格子暗号（Lattice-Based Cryptography）

格子暗号（Lattice-Based Cryptography）とは

「格子暗号（Lattice-Based Cryptography）」は、その名のとおり「格子」と呼ばれる数学的な構造を利用した暗号技術です。

現在、インターネット通信などに広く使われているRSA暗号や楕円曲線暗号（ECC）は、将来実用化が予測される量子コンピュータによって、容易に解読される可能性が指摘されています。この脅威に対応するために研究・開発されているのが、「ポスト量子暗号（PQC：Post-Quantum Cryptography）」です。

格子暗号は、ポスト量子暗号の中で最も有力視されている方式の1つです。量子コンピュータでも効率的な解法が発見されていない「格子問題」の難しさを安全性の基盤としており、その安全性と性能の高さから、次世代のスタンダードとして期待されています。

格子暗号の仕組み

格子暗号は、一見すると単純な点の集まりが、高次元になることで驚異的な複雑性を持つ「格子問題」を利用した暗号技術です。

暗号化では、平文に格子構造に基づくノイズを加えて暗号文を生成します。正当な復号するための鍵（秘密鍵）を持つ受信者のみが、このノイズを適切に除去して元の平文を復元できるという仕組みです。下図で示されている①の格子が秘密鍵、②の直交していない格子が公開鍵、送りたい文字と印とのずれがノイズとなります。

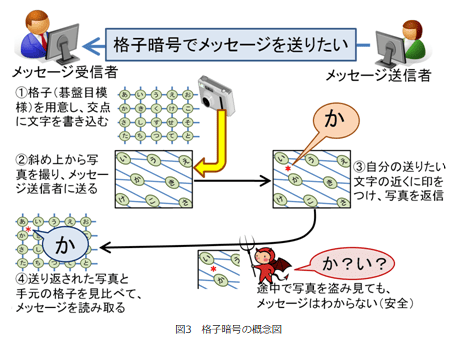
格子問題とは

格子とは、碁盤の目のように規則正しく並んだ「点の集合」を多次元空間に拡張したものです。2次元の格子（平面の格子）であれば、方眼紙の交点をイメージすると分かりやすいでしょう。

格子問題とは、この高次元の格子の中から「特定の性質を持つ点を見つけ出す問題」の総称です。代表的な格子問題に以下の3つがあります。

• 最短ベクトル問題（SVP：Shortest Vector Problem）：
  格子の中から、原点（一番中心の点）に最も近い点（原点以外）を見つけ出す問題
• 最近ベクトル問題（CVP：Closest Vector Problem）：
  格子の点ではない、空間上の任意の点を与えられたときに、そこから最も近い格子の点を見つけ出す問題
• Learning With Errors（LWE）問題：
  連立方程式に「小さな誤差」を加えたデータから、元の秘密ベクトルを復元する問題

低次元の格子であれば、これらの問題は比較的簡単に解くことが可能です。しかし、次元数が数百にもなると、問題の難易度は天文学的に跳ね上がります。仮に暗号文を第三者が取得したとしても、これらの問題を解けなければ解読は不可能というわけです。

なぜ量子コンピュータに強いのか

高次元の格子問題は、現在最先端のスーパーコンピュータや量子コンピュータを使っても、現実的な時間内に解く方法は見つかっていません。

現在主流の暗号技術であるRSA暗号や楕円曲線暗号（ECC）は、素因数分解や離散対数問題（※1）の計算困難性に基づいています。しかし、これらの問題はピーター・ショアが1994年に考案した「ショアのアルゴリズム」を用いて量子コンピュータで解読処理を行えば、短時間で解けることが数学的に証明されています。つまり、実用的な量子コンピュータが完成すれば、現在の暗号技術は瞬時に破られてしまうのです。

一方、格子問題は、ショアのアルゴリズムや既知の量子アルゴリズムでは効率的に解くことができません。この性質が、格子暗号が「量子コンピュータ耐性を持つ」と言われる理由です。

※1：ある数を何乗かした結果とその数の余りから、元の「何乗したか」という回数を求めることが計算困難である、という数学的な問題

格子暗号のメリットと課題

以上のように、格子暗号は高い安全性を持つポスト量子暗号の最有力候補です。しかし、実用化に向けた研究・開発段階の新しい技術であるため、メリットだけでなく、課題も存在します。

格子暗号のメリット

格子暗号の最大のメリットは、前述した量子コンピュータによる攻撃への耐性です。組織の機密情報や個人のプライバシーなど、長期にわたる保護が必要なデータを未来の脅威から守ることができます。

また、計算効率の高さもメリットです。ポスト量子暗号の候補には、他にも符号ベース暗号や多変数公開鍵暗号など、いくつかの種類がありますが、格子暗号は暗号化や復号の処理速度が比較的速く実用性に優れているとされています。

格子暗号の課題

一方で、格子暗号には実用化に向けて解決すべき課題もあります。

最も大きな課題は、鍵サイズと暗号文サイズの大きさです。従来の暗号技術と比較して、格子暗号の公開鍵や暗号文は数倍から数十倍のサイズになることがあります。そのため、ネットワーク帯域の消費量増加や、ストレージ容量の圧迫を引き起こすことが懸念されます。

また、長い歴史を持ち、世界中の研究者による厳しい安全性評価に耐えてきたRSA暗号に比べると、格子暗号は比較的歴史の浅い技術です。そのため、未知の攻撃方法が発見される可能性がゼロであるとは断言できません。この課題を克服するため、世界中の専門家が参加する標準化プロセスを通じて、継続的な安全性評価が行われています。

格子暗号の導入を検討する際には、メリットだけでなく課題も十分に理解しておくことが重要です。

格子暗号の今後の展望

格子暗号は、社会実装に向けた動きが世界的に加速しており、ITインフラの根幹を支える技術として普及する未来が近づいています。

この動きを主導しているのが、米国国立標準技術研究所（NIST）です。NISTは、ポスト量子暗号の標準化プロジェクトを2016年から進めており、世界中から応募された多数の候補アルゴリズムを、長年にわたって評価・選定してきました。2024年8月には、格子暗号を採用した「ML-KEM」「ML-DSA」を含む、3つのアルゴリズムを標準規格として公表しています。

これを受け、多くの企業や政府機関が格子暗号の採用を本格的に検討し始めており、今後数年のうちに広く導入が進むと見込まれています。

参考情報